4장. 다양한 분류 알고리즘 : 럭키백의 확률을 계산하라!
로지스틱 회귀
- 선형 방정식을 사용한 분류 알고리즘
- 시그모이드함수 (sigmoid fuction) 또는 로지스틱 함수 (logistic function) 사용
로지스틱 회귀로 이진 분류 수행
- 시그모이드 함수를 사용하여 z 를 0과 1 사이의 값으로 변환
로지스틱 회귀로 다중 분류 수행
- 소프트맥스 함수를 사용하여 여러 개의 z값을 확률로 변환
확인문제 2번 문제
- 로지스틱 회귀가 이진 분류에서 확률을 출력하기 위해 사용하는 함수
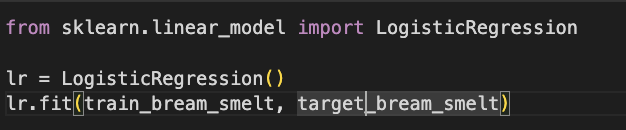
- 불리언 인덱싱을 통해서 도미(Bream)와 빙어(Smelt) 을 골라내기
- 해당 데이터로 로지스틱 회귀 모델 훈련
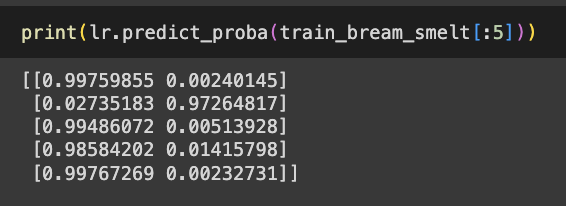
- 훈련한 모델을 사용해 train_bream_smelt에 있는 처음 5개 샘플 예측
- train_bream_smelt에서 처음 샘플의 예측 활률 출력
- 첫번째 열이 음성 클래스 (0) 에 대한 확률
- 두 번째 열이 양성 클래스(1) 에 대한 확률
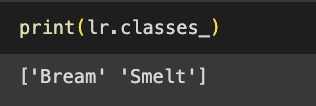
- bream, smelt 중 어떤 것이 양성클래스인지 확인
- classes_ 속성에서 확인
- bream →음성 클래스, smelt → 양성 클래스
- 여기에서 bream 를 양성 클래스로 사용하려면 bream인 타깃값을 1로 만들고 나머지 타깃값을 0으로 만들어 사용하면 됨
- 로지스틱 회귀가 학습한 계수 확인
- train_bream_smelt의 처음 5개 샘플의 z 값 출력
- LogisticRegression 클래스는 decision_function()메서드로 z 값 출력

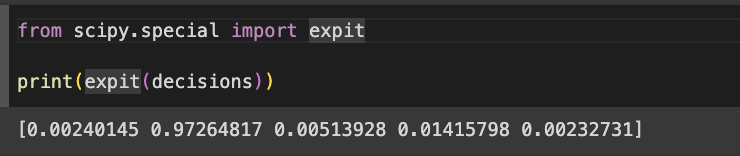
- z값을 시그모이드 함수에 통과시키면 확률을 얻을 수 있음
- 파이썬의 사이파이(scipy)라이브러리에 시그모이드 함수 사용 가능
확률적 경사 하강법
- 훈련 세트에서 샘플 하나씩 꺼내 손실 함수의 경사를 따라 최적의 모델을 찾는 알고리즘
- 샘플을 하나씩 사용하지 않고 여러 개를 사용하면 미니배치 경사 하강법이 됨
- 한 번에 전체 샘플을 사용하면 배치 경사 하강법
에포크
- 확률적 경사 하강법에서 훈련세트를 한번 모두 사용하는 과정
- 일반적으로 경사 하강법은 수십, 수백 번 이상 에포크를 수행
손실함수
- 어떤 문제에서 머신러닝 알고리즘이 얼마나 엉터리인지를 측정하는 기준
비용함수
- 훈련 세트에 있는 모든 샘플에 대한 손실함수의 합
로지스틱 손실 함수
- 양성 클래스(타킷 = 1) 일때 소실은 -log(예측 확률)로 계산, 음성 클래스 (타깃=0) 일때 손실은 -log(1-예측확률)로 계산
에포크와 과대/과소 적합
- 확률적 경사 하강법을 사용한 모델은 에포크 횟수에 따라 과소적합이나 과대적합이 될 수 있음
- 에포크 횟수가 적으면 과소적합, 너무 많으면 과대적합 문제가 발생
- 훈련세트 점수는 에포크 가 진행될수록 꾸준히 증가하지만 테스트 점수는 어느 순간 감소함
- 과대적합이 시작하기 전에 훈련을 멈추는 것이 조기 종료